О пользе дыхания

Вот кому может прийти такое в голову? Любой нормальный человек, а полиграфологи люди нормальные, понимает, что пользу от дыхания можно ощутить немедленно после того, как попытаться его задержать. И если до такого опыта польза может быть и не очевидна, то после уже никто из нормальных не будет в нёй сомневаться. Но вы зашли в гости к ненормальному полиграфологу. А у ненормального и мысли ненормальные. Поэтому он запросто может предложить Вам изучать насколько полезно дыхание, и даже дать числовую оценку полезности. Но для этого нужны инструменты. У нормального полиграфолога в инструментах числятся экспертные баллы, а у ненормального должно быть что-то своё - ненормальное. Ну раз должно, то и есть - алгоритмы классификации. А ещё есть данные, выборки метрических данных тестов. Есть российская выборка - данные 200 - т тестов, и американская - 100 тестов. Взял ненормальный полиграфолог и посчитал какой вклад в решение алгоритма вносит такой признак физиологической реакции как ДЛГД (длина линии грудного дыхания). Для алгоритма это, например, значение лямбды дыхания. Если по результатам теста лямбда положительна, то это ложится в копилочку решения алгоритма в сторону правдивости ответов, если отрицательна - в сторону лживости. А вот в OL наоборот если "сила реакции" положительна, алгоритм склоняется в сторону лживости, и, если отрицательна - в сторону правдивости. Ну а с Б7 предельно ясно. Баллы они и в Африке баллы. В общем, я вчера посчитал все значения лямбд, "силы реакции", баллов по дыханию из выборок, разбив их на полезные и вредные. Вставляйте спички в глаза и давайте займёмся ненормальным - изучим полученные данные и сделаем выводы. Вот они эти данные в табличках

Если посмотреть внимательно, то можно увидеть, что соответствующие числа в ячейках таблиц Сокола и OL для одной и той же выборки достаточно близки между собой, а для разных выборок находятся в примерно одинаковой пропорции. Так и должно быть. Точность алгоритмов близка, коэффициент контингенции близок к единице, и было бы удивительно, если б числа в таблицах для дыхания различались существенно. Про разные выборки можно сказать аналогично. И там, и там полиграммы с известным решением, а правдивые и лживые в них в одной и той же пропорции - 50 на 50. И получается, что проживающие в "граде на холме" и в наших суровых действительностях, дышат одинаково. Что лживые, что правдивые. Давайте проверим это предположение. Проверить это важно с политической точки зрения. Неужели толерантные демократы дышат так же, как и суровые обитатели Мордора? Используем для проверки наш верный Хи2. И сделаем это сначала для общего количества положительных и отрицательных значений алгоритма Сокол. Чем воспользуемся? Такой зверь как Excel живёт у каждого нормального полиграфолога в ноутбуке. Поэтому, несмотря на ненормальность хозяина, будем им и пользоваться. Предположим, что так и есть: американцы и россияне в дыхании реагируют на стимулы одинаково. То есть обе выборки взяты из одного распределения (одной генеральной совокупности). Исходя из этого предположения, построим ожидаемые частоты. Не спать в гостях! Итак, приступаем.

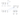
Справились. Теперь давайте посмотрим насколько далеко те числа, которые мы наблюдаем отклоняются от тех, что мы ожидаем для того случая, когда толерантовцы дышат в "унисон" с мордоровцами. Если слишком далеко, мы сделаем вывод, что в "унисон" это не верно, а верно быть может в "противофазе". Воспользуемся функцией ХИ2.ТЕСТ. Она выдаст нам число, которое называется "достигаемый уровень значимости" или p-value, если ваш выбор - демократия. Сейчас уже самый гуманитаристый гуманитарй знает, что если это значение меньше 0,05, то с тем предположением, которое проверяется надо расставаться. Так открываю функцию и что же нам засыпать в неё в качестве аргументов?

Хи2 выдал нам значение p-value равное 0,56. Это значит нет никакого основание отказаться от предположения, что и американцы, и россияне дышат в "унисон". Да, но надо ещё проверить это предположение отдельно для правдивых и лгущих опрашиваемых.

Ну вот и лживые, и правдивые, и российские, и американские реагируют дыханием на стимулы в ТВС одинаково. Теперь мы законным образом объединить обе выборки в одну. Полная дружба народов! Надо Путину с Байденом сообщить. Быть может тоже в "унисон дышать" будут. Но мы не проверили ещё кое-что. Догадались? Мы не проверили: а может быть правдивые и лживые в дыхании реагирую одинаково? Ну что ж используем опять-таки наш верный Хи2.

Хи2 выдал достигаемый уровень значимости равный нулю до второго знака. Можно делать вывод, что те, кто лжёт и те, кто говорит правду дышат по-разному! Вот теперь можно поговорить о пользе дыхания. Что значит польза в нашем случае? А это значит, что дыхание вносит существенный вклад в решение алгоритма. И вклад этот должен быть в правильное решение. Иначе это не польза получается, а один вред. А когда ни вреда, ни пользы? Это когда вклад может быть с одинаковой вероятностью как полезный, так и вредный. То есть, если знак лямбды дыхания, в результате теста, с одинаковой вероятностью может быть как положительный, так и отрицательный. Иначе говоря, вероятность 0,5 — это ни вреда, ни пользы. Это значит, что тип вопроса в сравниваемой паре не влияет на ДЛД. А что с нашими данными? О чём они говорят? Есть польза от дыхания, или всё-таки нет? А вдруг, то неравенство частот, что мы видим всего лишь игра его величества случая, а вероятность знака лямбды дыхания всё-таки равна 0,5 - нет связи дыхания с типом вопросов и лживостью ответов? Проверим это. Для проверки используем широко известный факт, что вот такая штука - t, при объёме выборки n не менее ста, имеет стандартное нормальное распределение. m — это количество случаев, когда лямбда дыхания теста причинила пользу - сделала положительный вклад в правильное решение. Для правдивых m = 93, а для лживых 119. Надеюсь, это понятно? ...Так, так, глаза разлепи, гость, спать на пенсии будешь, когда ресурс выработаешь..., проверим гипотезу о том, что p = 0,5 (ни вреда, ни пользы) сначала для правдивых. Для этого сосчитаем t

Теперь можно использовать функцию Excel - НОРМ.РАСП. Подставим в неё полученное значение t для правдивых. Да. Вот ещё, что: так как мы проверяем правостороннюю альтернативу (о том, что от дыхания польза, а точно не вред) мы должны полученное значение вычесть из единицы. Таким образом мы и получим то, что нам надо, а именно p-value.

Замечательно! Можно однозначно утверждать, что польза от дыхания для определения правдивых есть! Вот правда ещё надо посмотреть насколько велика эта польза. Это сделаем чуть позже, сначала вычислить t и p-value для лжецов. Делать надо всё точно так же, за исключением того, что в формулу подставить 119 вместо 93. Получим t = 9,20. А для значения p-value значение практически не отличимое от нуля. Польза от дыхания для "поимки" лжецов однозначно есть! Теперь оценим пользу от дыхания для правдивых и лжецов. Получим её оценку как оценку вероятности того, что дыхание внесёт положительный вклад в решение алгоритма. А такую оценку сделать очень просто:

Величина пользы от дыхания для определения правдивого

P = 93/150 = 0,62

Величина пользы от дыхания для определения лжеца

P = 119/150 = 0,79

ОГО! Польза от дыхания для поимки лжеца заметно больше, чем для определена правдивого. Для правдивого она есть, но совсем незначительно ушла от бесполезности, а то и вреда. Примерно в сорока процентов случаев дыхание правдивого опрашиваемого будет вносить отрицательный вклад в решение алгоритма. В случае дыхания обманщика это число в 2 раза меньше - дыхание лжеца только в двадцати процентов случаев внесёт трицательный вклад в решение алгоритма.

Ну ладно. Если ты дочитал до этого места, то никому не рассказывай! А то и тебя посчитают ненормальным. А в следующий раз, если надумаешь заглянуть ко мне - оглядывайся. Вдруг за тобой кто-нибудь пристально наблюдает!